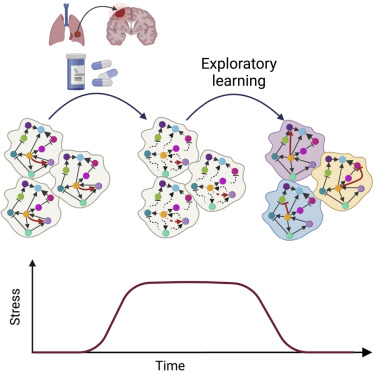
Defining many different phenomena as “learning” has both merits and dangers.
On the one hand, stretching the definition to claim that learning how to solve an integral is identical to chemotaxis in bacteria might not be too useful. On the other hand, recognizing common themes among different “learning” systems can provide several benefits.
First, there could be general principles that transcend specific systems. These can include exploration, gradient descent, degeneracy and redundancy.
Second, there could be historical accidents that bias certain fields with no “organic” reason. For instance, both regulatory genetic networks and neural networks are high-dimensional dynamical systems. They involve many elements that interact and change over time. The technology that started electrophysiology (single electrode recordings) emphasized the dynamics of a single element. The technology in genetic networks (e.g., DNA chip) emphasized a static snapshot of multiple elements. Both fields acknowledge the high-D dynamic nature of the biology. Yet, it took a long time for neuroscience to consider populations of neurons, and for genetic networks to emphasize dynamics.
Third, these technological differences can make it easier to observe certain facets of learning in one system and not another.
Below are a few examples of attempts to make such links. More are in progress.
Mathematical models of learning and what can be learned from them

